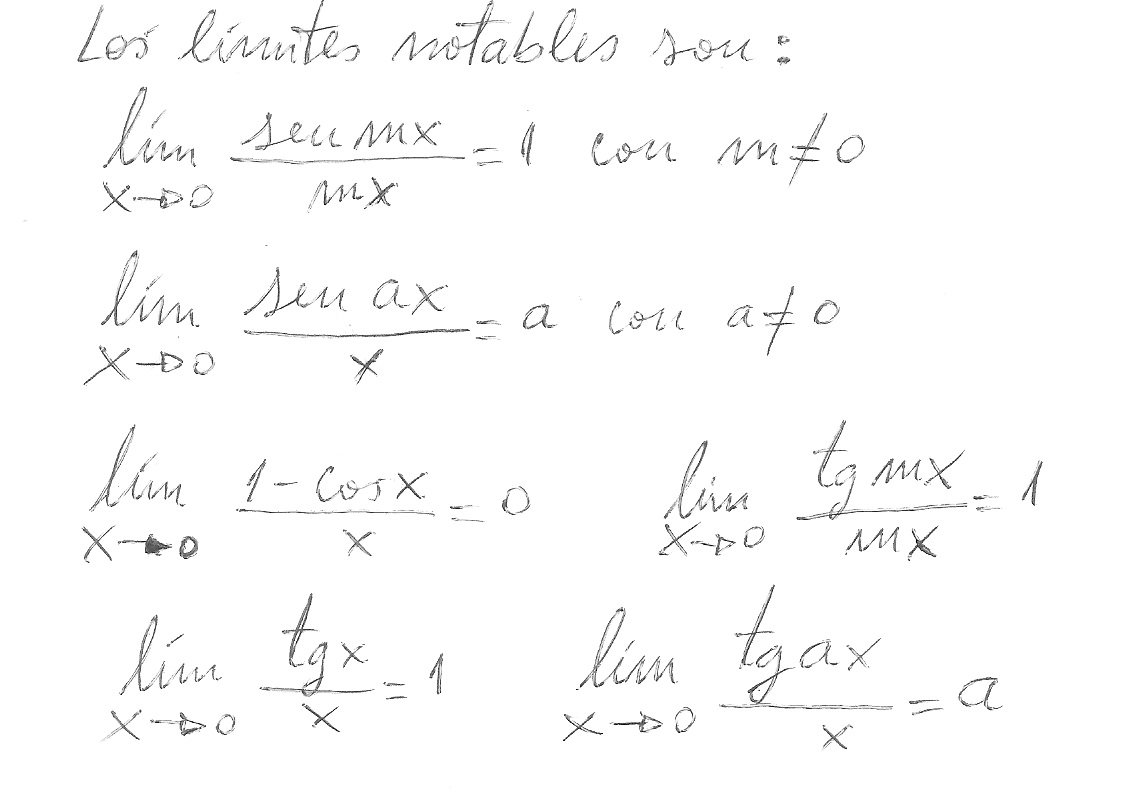L í m i t e s T r i g o n o m é t r i c o s
Resulta indispensable conocer las funciones trigonométricas como Seno, Coseno y Tangente. Comencemos por el límite trigonométrico fundamental:

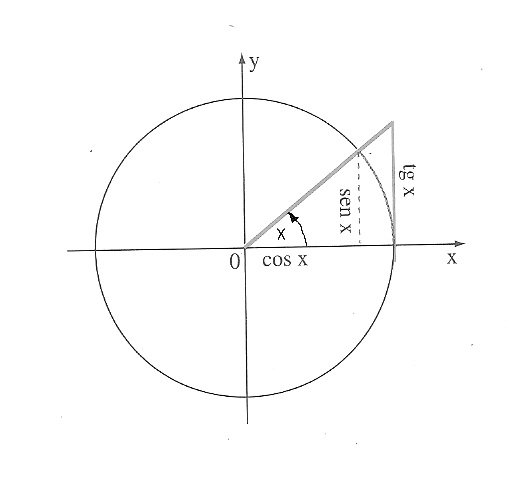
Vemos claramente que el sen de x es menor que la tg de x, eso significa que cualquier valor asignado a x resultará siempre mayor la tangente que el seno del ángulo comprendido entre 0,111 y 89,999, recuerde sen90°= 1 y la tangente de 90°(π/2) no existe. El único caso en que el seno se igualará con la tangente es cuando x valga 0 porque sen0°=0 y tg0°=0.
Podemos iniciar la demostración del límitetrigonométrico fundamental con la desigualdad
(senx/x) < (tgx/x) simplifico x en ambos miembros y luego reemplazo tgx por senx/cosx ya que tgx=senx/cosx
(senx)<(senx/cosx) divido senx en ambos miembros
(senx/senx)<[(senx)/(cosx.senx)] en donde senx también se simplifica resultando
1<(1/cosx) como cos0°=1 al aplicar el límite cuando x tienda a 0 quedará 1/1 es igual a 1 y así se verificó.