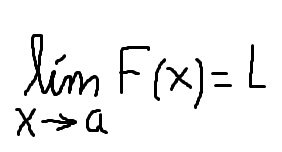
L I M I T E S
En una función F(x) analizamos el comportamiento de la gráfica en un determinado punto de coordenadas (x,y). Tomando un determinado valor por el cual se aproxime la función cuando "x" tienda a ese valor, analizamos si existe o no el límite L. De acuerdo a esta definición se escribe:
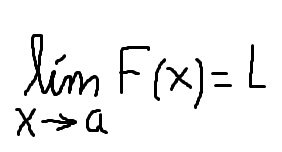
Ejemplo: analicemos el comportamiento de la función 2x+1 cuando "x" tienda al valor 1 a ver si existe o no:
F(x) = 2x+1 a = 1 aplicando límite cuando x tiende a 1 nos queda:
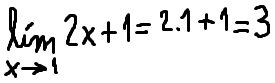
Realice ud. solito el gráfico correspondiente a la función 2x+1 para una mejor interpretación en un par de ejes de coordenadas. Es decir, existe el límite de dicha función para x tendiendo a 1 y es igual a 3.
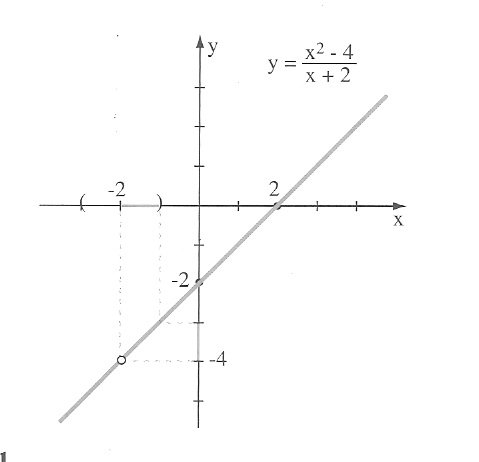
Si el resultado del límite hubiese sido una indeterminación (0/0) significa que para ese punto en particular habría un punto vacío en el trazado de la gráfica. Otro caso sería, si al llegar al resultado casi final, tenemos un número cualquiera dividido en cero, obtenemos el famoso "infinito" y eso significa que en ese punto al cual tiende x la función crece o decrece infinitamente hacia una "asintota vertical" por lo tanto no existe el límite en ese punto al cual tendía x.
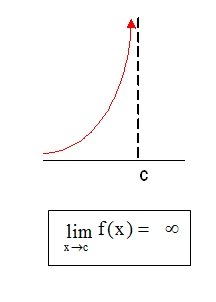
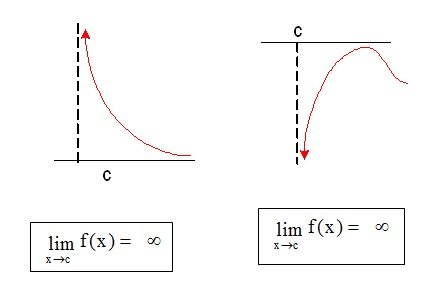

¿Analizamos qué ocurre en el límite del siguiente ejemplo cuando x tienda a -2 y cómo salvaríamos la indeterminación factorizando?